Lewary są to przewody zamknięte służące do przeprowadzania cieczy z położenia wyższego do niższego nad przeszkodą.

Rys. 1. Schemat lewara
Rysunek 1 przedstawia konstrukcję lewara służącego do przeprowadzania wody z wyżej położonego zbiornika A do zbiornika B położonego niżej. Lewar C składa się z dwóch odcinków. Na pierwszym odcinku zanurzonym w zbiorniku A ciecz zostaje przez podciśnienie (zassanie) podniesiona na poziom c-c, wyższy niż w zbiorniku A (na wysokość Hs). Na odcinku drugim natomiast ciecz spływa pod wpływem własnego ciężaru z poziomu c-c wyższego od poziomu a-a do poziomu b-b położonego niżej od a-a. Aby w lewarze rozpoczął się i odbywał przepływ cieczy, trzeba najpierw wytworzyć w pierwszej części lewara podciśnienie przez wyssanie powietrza z górnej części lewara (np. za pomocą pompy powietrznej). Wskutek tego ciecz ze zbiornika A wznosi się do poziomu c-c i osiągnąwszy najwyższy punkt lewara przelewa się przez prawe ramię do zbiornika B. Przepływ cieczy ustaje w lewarze z chwilą, kiedy poziomy w obu zbiornikach wyrównają się.

Fot. 1. Widok lewara
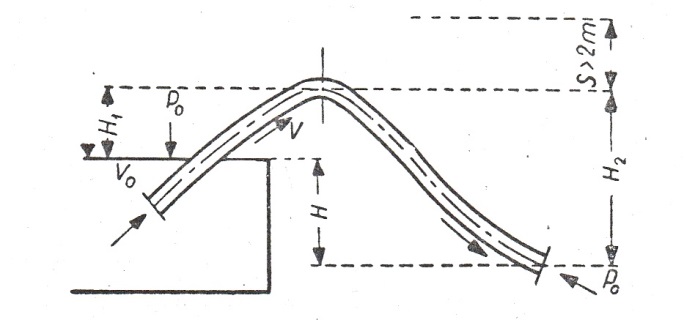
Rys. 2. Schemat obliczeniowy lewara
Układając równanie Bernoulliego dla odcinka pierwszego należy pamiętać o tym, żeby nie nastąpiło przerwanie strugi. Wysokość ciśnienia musi być większa od zera, a zatem:
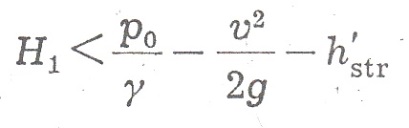
Wysokość podnoszenia wynosi 7—8 m, a praktycznie H1≤ 6 m. Stosunki energetyczne na odcinku drugim określa również równanie Bernoulliego, a ponieważ p : γ ≥ 0, dlatego :

W odniesieniu do poziomu morza można zapisać : H2 < 10,33 + hstr
czyli największą dopuszczalną wysokość opuszczania cieczy z poziomu ponad przeszkodą do poziomu otworu wylotowego.
Prędkość przy wypływie z lewara oblicza się z równania:
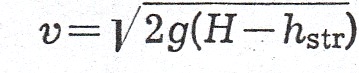
gdzie: hstr — suma strat przy przejściu cieczy przez lewar.
Po obliczeniu strat lokalnych równanie przybiera postać:
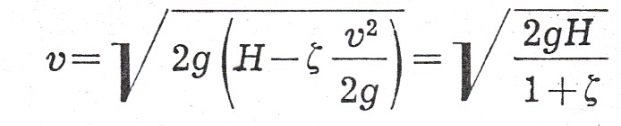
gdzie : ζ — współczynnik oporu zależny od konstrukcji i materiału lewara.
Zamiast współczynnika oporu można przyjąć do, obliczeń współczynnik sprawności lewara identyczny ze współczynnikiem wydajności wypływu przez otwór w naczyniu, gdzie :
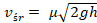
Przyrównując to .równanie do równania na prędkość wypływu z lewara otrzymamy

oraz

Równania te określają zależność między współczynnikiem oporu i sprawności (wydatku).
Przepływ odbywa się pod wpływem różnicy wysokości w obu zbiornikach. Ponieważ prędkość v1 z jaką ciecz wypływa ze zbiornika A, jest mała, a tym samym i wysokość prędkości v2/2g jest nieznaczna, można na podstawie równania Bernoullego przyjąć, że
Δh = ΣhA-B
gdzie: ΣhA-B - suma strat naporu wzdłuż całego lewara.
Ponieważ opory miejscowe są również zależne od wysokości prędkości, można je jako małe pominąć. Wydatek lewara określa się więc z wzoru :
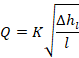
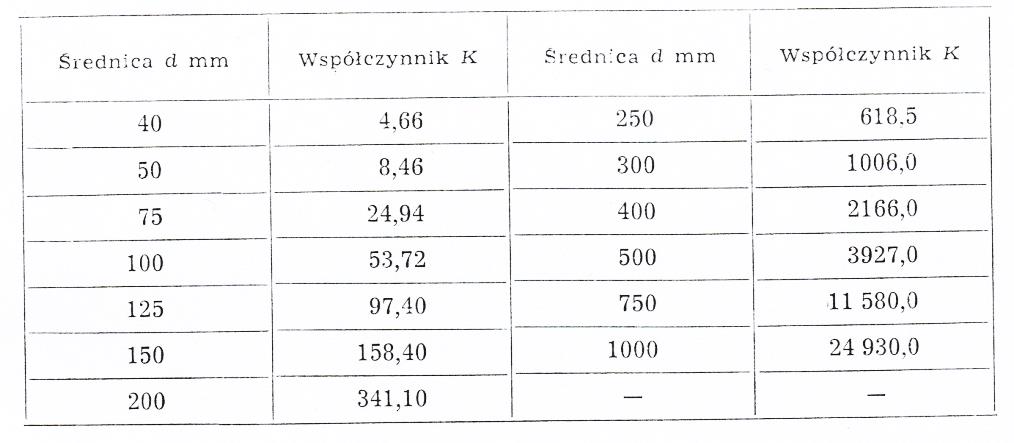
gdzie: K - współczynnik wydatku podany dla przewodów żeliwnych w tab. 1,
hl /l - spadek hydrauliczny.
Tab. 1. Współczynniki wydatku K dla przewodów żeliwnych
Lewary są często stosowane w praktyce jako części składowe urządzeń hydrotechnicznych, do przeprowadzania (bez użycia pomp) ropy naftowej itp. produktów z cystern kolejowych lub samochodowych do zbiorników, do przeprowadzania przewodów wodociągowych na mostach ponad ciekami itp. W wodociągach stosuje się urządzenia lewarowe do przeprowadzenia wody ze studni zasilających do studni zbiorczej przy ujęciu wody do wodociągu lub ze zbiorników wodnych otwartych dla regulacji ustalonych poziomów.
Sprawne działanie lewarów zależy od:
- odpowiedniej różnicy poziomów zwierciadła cieczy w zbiorniku zasilającym i zbiorniku pobierającym (położonym niżej),
- od szczelności przewodów oraz
- od tego, by rozrzedzenie powietrza w przewodach ssawnych nie było nadmierne, bo wtedy para wodna wydobywając się z wody może spowodować rozerwanie strumienia wody w lewarze i zatrzymanie przepływu.
Powietrze wydobywające się z wody w postaci drobnych pęcherzyków zwiększa opory ruchu, stąd więc straty naporu obliczone dla dłuższych lewarów przy użyciu zwykłych wzorów hydraulicznych należy zwiększyć o 15 ÷ 20%.
Literatura:
- Linder F.: Budowa mostów. Cz. 1. PWSZ, Warszawa 1970 r.,
- Kollis W. [i in.]: Przewodnik budownictwa wodno-melioreacyjnego. Tom I. PWRiL. Warszawa 1955 r.