Znajomość rodzaju panującego ruchu cieczy wewnątrz przewodu zamkniętego, posiada bardzo istotne znaczenie w praktyce hydraulicznej i hydrotechnicznej. Podczas przepływu cieczy rzeczywistej występują siły tarcia wewnątrz samej cieczy i w sąsiedztwie ścian przewodu. Straty te przekładają się w sposób wymierny na zużycie energii podczas pompowania oraz na awaryjność urządzeń i sieci transportujących ciecze.
W sieciach wodociągowych straty hydrauliczne wynikają z prędkości cieczy podniesionej do kwadratu. W obliczeniach praktycznych korzysta się przeważnie z dolnej prędkości granicznej. Nie jest to jednak dogodnym wskaźnikiem do porównań rodzaju ruchu w przewodach o różnych kształtach przekroju poprzecznego, gdyż średnia prędkość przepływu nie zależy tylko i wyłącznie od średnicy przewodów.
Liczba Reynoldsa dla przewodów okrągłych wynosi :
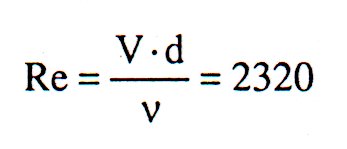
gdzie :
V – średnia prędkość przepływu cieczy w przewodzie okrągłym, m/s
d - średnica przewodu, m
ν - kinematyczny współczynnik lepkości, m2/s
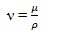
gdzie :
μ – współczynnik proporcjonalności zw. dynamicznym współczynnikiem lepkości lub też lepkością cieczy,
ρ - gęstość cieczy, kg/m3
Liczba Reynoldsa jest wskaźnikiem do ustalania momentu przejścia cieczy z ruchu laminarnego w burzliwy :
- Re ⩽ 2320 - w przewodzie panuje zawsze ruch laminarny,
- Re ⩾ 2320 - w przewodzie przepływ jest burzliwy lub laminarny w zależności od warunków badawczych,
- Re > 50000 - panuje wyłącznie ruch burzliwy.
Dolna granica prędkości średniej, przy której następuje zmiana charakteru ruchu wynosi dla rurociągów o średnicy 0,20 m i w temperaturze 10oC, odpowiednio:
- dla oliwy o ν = 0,00015 m2/s Vgr = 1,74 m/s
- dla wody o ν = 0,000001306 m2/s Vgr = 0,015 m/s
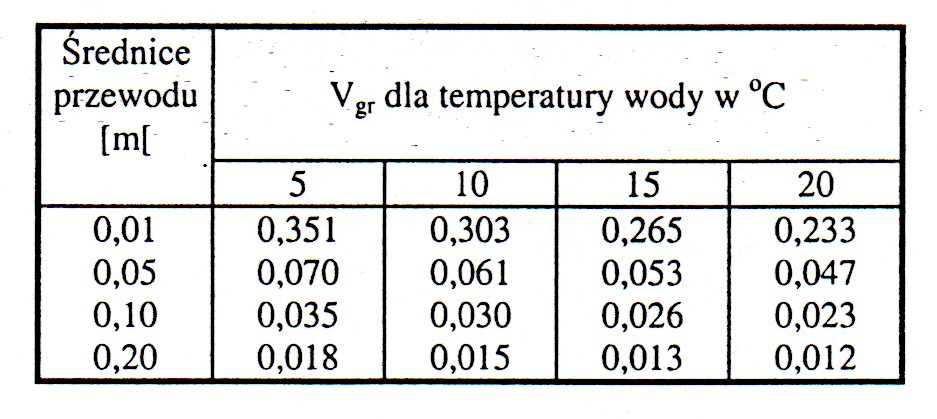
Wniosek: o zmianie charakteru ruchu w rurociągu decyduje wartość ν oraz, że w przewodach wodociągowych dominującym jest ruch burzliwy, gdyż średnie prędkości przepływu wynoszą tam ok. 1,0 m/s. Wpływ temperatury wody na średnie prędkości graniczne wody płynącej w rurociągach o różnych średnicach przy Re = 2320, przedstawiony jest w tabeli :