Ruch zmienny w korytach otwartych jest to ruch, przy którym powierzchnia przekroju i prędkości przepływu zmieniają się w różnych punktach na długości liniowej strumienia. Powstaje tu zatem zmiana prędkości średniej strumienia. Rozróżnia się dwa rodzaje ruchu zmiennego:
- przyspieszony i
- opóźniony.
Najczęściej spotykanymi przyczynami powstawania ruchu zmiennego są zmiany przekrojów poprzecznych koryta, napełnienia i prędkości, spowodowane nagłym obniżeniem się (np. na stopniu) lub podniesieniem zwierciadła wody (np. przez zwężenie lub przegrodzenie koryta budowlą piętrzącą) w porównaniu z napełnieniem normalnym, stanem morza w strefie ujściowej rzeki oraz parciem wiatru.
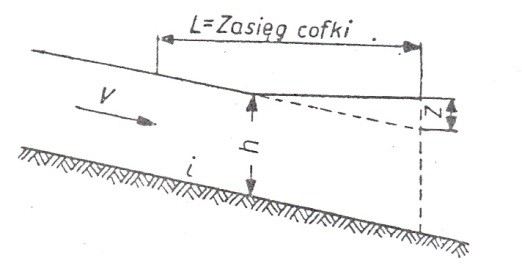
Rys. 1. Zasięgiem spiętrzenia (cofki)
W tym przypadku powstaje spiętrzenie zw. wody, które układa się według krzywej spiętrzenia (rys. 1). Zasięg tej krzywej nazywamy zasięgiem spiętrzenia albo zasięgiem cofki lub po prostu cofką. W praktyce obliczenie cofki jest niezmiernie ważne, m. in. z uwagi na obwałowania ppow. rzeki na odcinku cofkowym, stwierdzenie możliwości podtopienia terenów nadrzecznych i ich zasięgu, trudności w żegludze itp. Przyjmując schematycznie kształt cofki jako parabolę 2 stopnia, można ustalić przybliżone równanie na długość cofki w postaci:
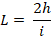
gdzie: h - wysokość piętrzenia, i - naturalny spadek zw. wody (przed zakłóceniem). Do dokładnego obliczenia cofki służą odpowiednie wzory i tabele, oparte na właściwościach ruchu zmiennego. Wzór Ruhlmanna do obliczania cofki w korytach o przekroju prostokątnym:
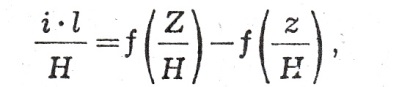
gdzie: i - spadek zw. wody niespiętrzonej,
l - odległość od początku cofki do przekroju badanego,
H - normalne napełnienie koryta,
Z - spiętrzenie (depresja) na początku cofki,
z- spiętrzenie (depresja) w przekroju badanym.
Tab. 1. Wartość funkcji do obliczenia krzywej spiętrzenia dla koryt prostokątnych (wg Ruhlmana)

Zasięg cofki obliczamy ze wzoru:
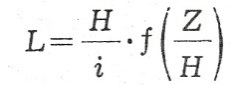
Wzór Tolkmitta do obliczania cofki w korytach o przekroju parabolicznym:
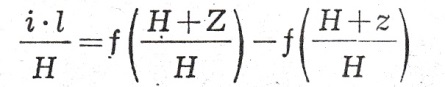
oraz obliczania zasięgu cofki:
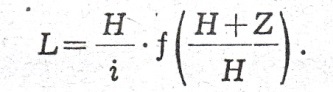
Tab. 2. Wartość funkcji do obliczenia krzywej spiętrzenia dla koryt parabolicznych (wg Tolkmitta)
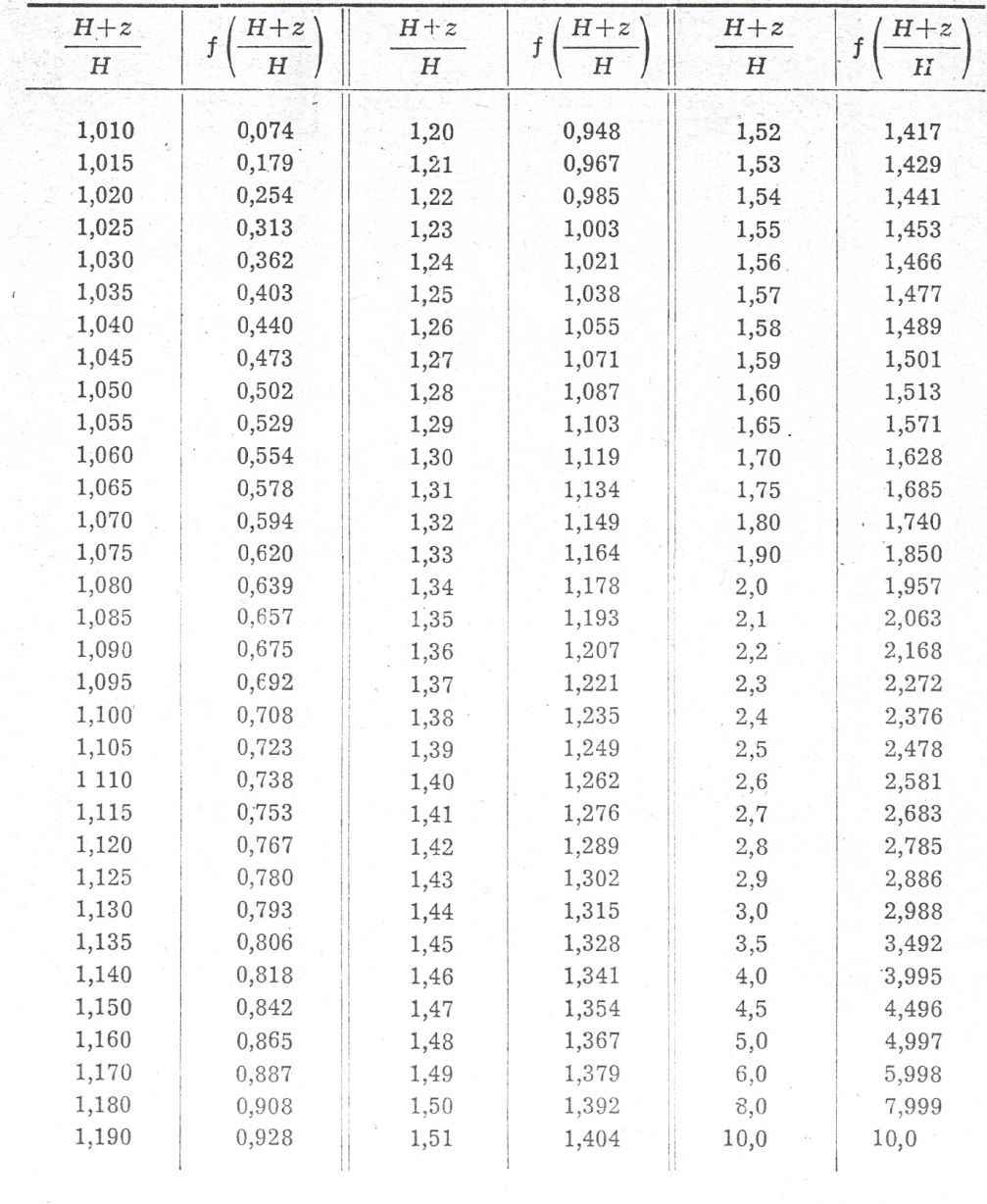
Obliczenia cofki w korytach nieregularnych dokonujemy przez obliczanie różnic poziomów na odcinkach skończonych (rys. 2).
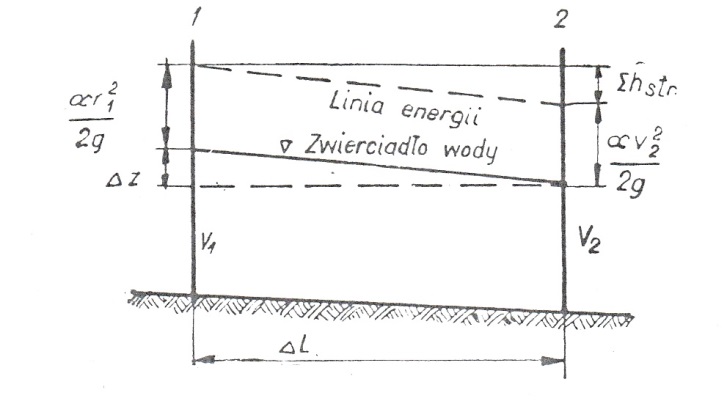
Rys. 2. Odcinek skończony do obliczeń cofki
Różnice poziomów linii energii na badanym odcinku zużywa się na pokonanie oporów na tym odcinku:
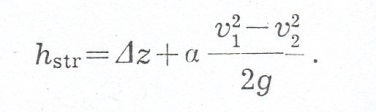
Ponieważ strata na długości L wynosi :
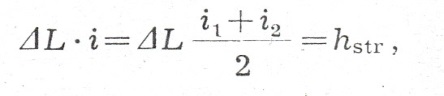
przez to:

równanie różnicowe wartości spadków można obliczyć po przekształceniu wzoru
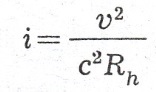
lub ze wzoru Matakiewicza
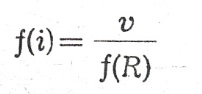
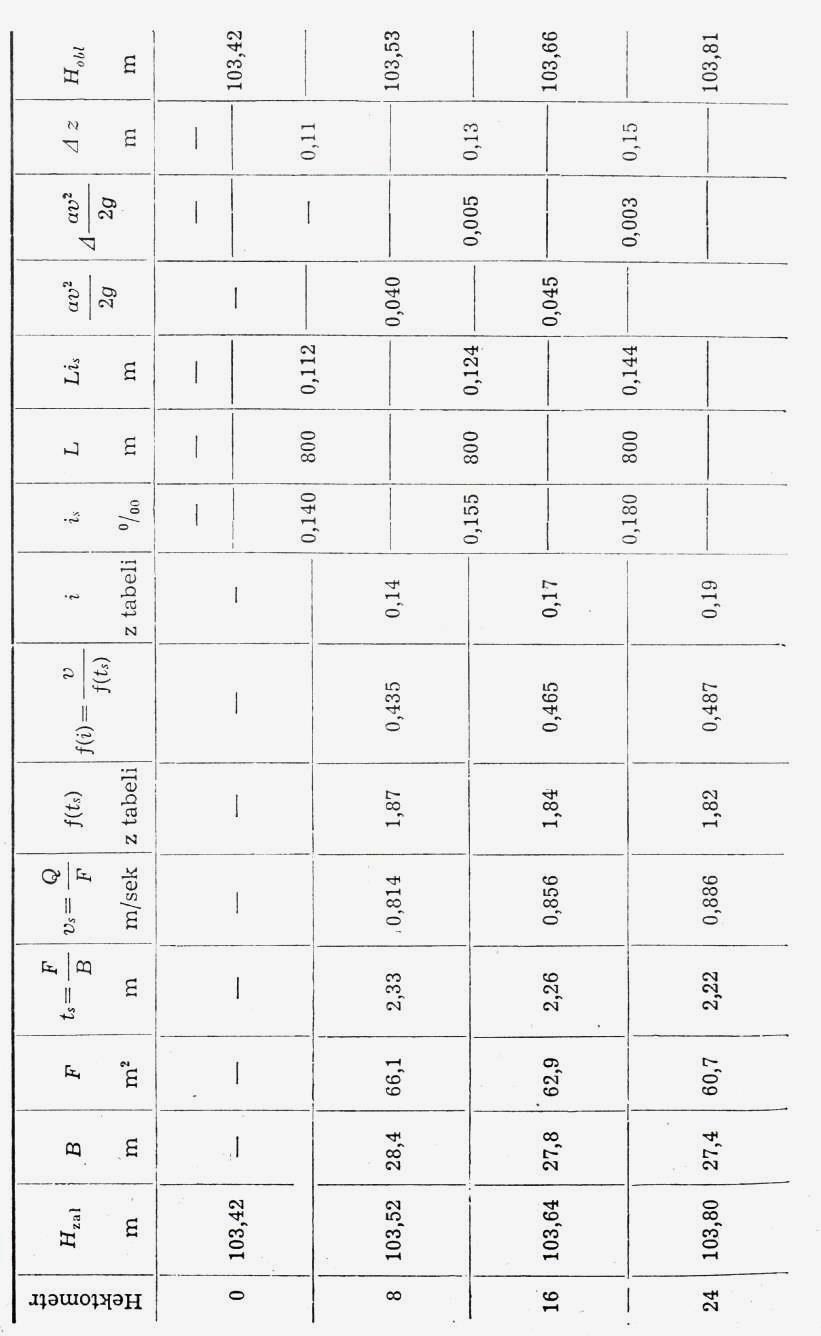
Obliczanie cofki rozpoczyna się od przekroju początkowego (miejsce powstania cofki) obliczając poszczególne elementy tego przekroju (F, B, ts, v, i) i przechodząc następnie do przekroju leżącego wyżej w odległości ΔL, której wielkość przyjmujemy zależnie od wymaganej dokładności w obliczeniu rzędnych cofki. Należy pamiętać, aby poszczególne odcinki zawierały przekroje zbliżone do siebie kształtem.
Z kolei przechodząc do następnego odcinka i zakładając w przybliżeniu rzędną zw. wody przeprowadzamy obliczenie analogiczne do poprzedniego. Obliczona rzędna zw. wody powinna zgadzać się z rzędną założoną (błąd dopuszczalny wynosi ±2 ÷ ±3 cm). W przypadku niezgodności powtarzamy obliczenie przy założeniu innej rzędnej. W ten sposób ustalamy rzędne zw. wody w następnych przekrojach aż do końca cofki, a praktycznie do miejsca, w którym spiętrzenie (depresja) wynosi 2—3 cm. Obliczenie najdogodniej jest przeprowadzać tabelarycznie według przykładu (tab. 3).
Tab. 3. Tabelaryczne obliczanie cofki w korytach nieregularnych