Przelewem nazywa się przegrodę umieszczoną w kanale lub korycie wstawioną w strumień cieczy lub rzeki o swobodnym zwierciadle. Przegroda taka powoduje piętrzenie strumienia i doprowadza do przelewania się wody przez koronę. Odległość dna kanału od korony konstrukcji przelewu stanowi wysokość przelewu. Per analogia, przelewem nazwiemy także wypływ z dużego otworu w przypadku gdy zwierciadło cieczy w dolnym stanowisku jest położone poniżej korony (krawędzi) otworu. Przelewy stosuje się w hydrotechnice, urządzeniach sanitarnych i melioracyjnych jako:

•  zapory,
•  jazy,
•  zastawki,
•  burzówki,
•  w oczyszczalniach ścieków jako urządzenia napowietrzające,
•  w stacjach uzdatniania wody,
•  urządzenia do pomiaru wydatku (wystarczająca jest np. deska o długości > 2,0 m).

Klasyfikacja przelewów wymaga szczegółowego opisu podstawowych cech przelewów.
Ze względu na przekrój ścianki przelewu:

•  przelewy o cienkiej ściance i ostrej krawędzi

Przelewy o ostrej krawędzi stanowią cienką ściankę zazwyczaj ściętą od strony dolnej wody. Gdy istnieje dopływ powietrza między ścianką a dolną powierzchnią strumienia, wówczas funkcjonuje on prawidłowo jako swobodny, w którym strumień nie przylega do ścianki. Mamy tu do czynienia z rzutem strumienia. Aby uzyskać taki strumień w przelewach bez bocznego dławienia (przy n = 0) należy poniżej strumienia wprowadzić rurkę perforowaną doprowadzającą powietrze.

•  przelewy o szerokiej koronie

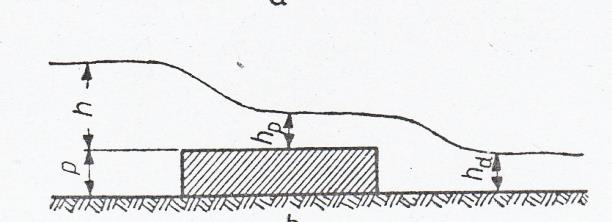
Przelewy o szerokiej koronie umożliwiają uzyskanie ruchu wolnozmiennego, w którym strugi są nieomal równoległe. Niezbędne do tego jest aby szerokość korony przelewu δ względem wysokości piętrzenia h wynosiła δ > (2 - 3)h.

•  przelewy o kształtach praktycznych

Przelewy o kształcie praktycznym zapewniają cieczy opływanie górnej powierzchni przelewowej, minimalizując obciążenie i oderwanie się od niej strumienia. Jest to typowe działanie przeciw wystąpieniu groźnego zjawiska kawitacji.

Do prawidłowego wyprofilowania takiej powierzchni istnieją tablice współrzędnych, np. Creagera, które będą przedstawione w dalszej części.

Warunkami koniecznymi dla klasyfikacji przelewów w tym zakresie są kryteria szerokości korony przelewu:

•  przelewy o ostrej krawędzi                                   δ  <  0,5 H
•  przelewy o szerokiej koronie              2,5 H   <   δ  <  15 H
•  przelewy o kształtach praktycznych   0,5 H   ⩽   δ  ⩽  2,5 H

gdzie:   δ – szerokość korony przelewu,
            H – wzniesienie zwierciadła wody w górnym stanowisku ponad koronę przelewu,
           p_g  - wysokość progu od strony górnej wody,
           p_d  - wysokość progu od strony dolnej wody,
           v_o  - prędkość przepływu,
           v_o²/2g   - wysokość prędkości.

W literaturze tematu, zwłaszcza w pozycjach starszych, spotkać można zamiast granicy (0,5 H) to (0,67 H).
Ze względu na położenie zwierciadła wody dolnej:

•  przelewy niezatopione — poziom zw. wody dolnej nie wpły­wa na wydajność przelewu

•  przelewy zatopione — poziom zw. wody dolnej wpływa na wydajność przelewu

Dla poszczególnych rodzajów przelewów o różnych kształtach warunki zatopienia lub też niezatopienia można przedstawić w formie graficznej z oznaczeniami zw. wody dolnej:

Rys. 1. Przelewy – niezatopione (a, b, c) i – zatopione (d, e, f)

Dla przelewów o szerokiej koronie można zastosować dwa warunki konieczne:

Rys. 2. Przelew o szerokiej koronie

•  wysokość a_e < a     – przelew niezatopiony, gdzie :     a = 2/3 h_o
•  wysokość a_e > a      - przelew zatopiony, gdzie :     a = 2/3 h_o

Przy czym :  

Ze względu na kształt wycięcia:

•  przelewy prostokątne (rys. 3a),
•  przelewy trapezowe (rys. 3b),
•  przelewy trójkątne (Thomsona)  (rys. 3c),
•  przelewy półkoliste (rys. 3d)

Rys. 3. Kształty wycięcia w przelewach

Ze względu na położenie w planie:

•  przelewy proste (rys. 4a),
•  przelewy ukośne (rys. 4b),
•  przelewy łamane zaprądowe (rys. 4c)
•  przelewy łamane przeciwprądowe (rys. 4c’),
•  przelewy krzywoliniowe (rys. 4d),
•  przelewy boczne (rys. 4e)

Rys. 4. Kształty przelewów w planie

Ze względu na szerokość przelewu w stosunku do szerokości koryta:

• przelewy bez bocznego dławienia (kontrakcji bocznej) (rys. 5a),
• przelewy z bocznym dławieniem jednostronnym (rys. 5b),
• przelewy z bocznym dławieniem dwustronnym (rys. 5c)

Rys. 5. Podział przelewów ze względu na dławienie przepływu

Porównując długość korony przelewu b z szerokością koryta B zauważyć można istnienie dławienia bocznego strumienia. Przy braku dławienia n = 0, przy dławieniu jednostronnym n = 1, a przy dławieniu obustronnym n = 2. Te czynniki będą wykorzystane przy opisie obliczeń hydraulicznych wydatku przelewów.
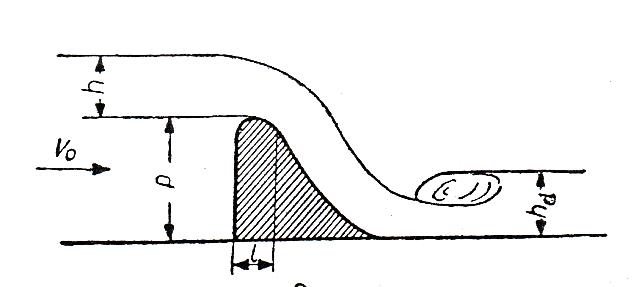
Przelew swobodny występuje wtedy, kiedy przestrzeń między wypływającą strugą a ścianą przelewu (a) wypełniona jest powietrzem o ciśnieniu atmosferycznym (rys. 6).

Rys. 6. Przelew swobodny z przestrzenią powietrzną

Obliczenia hydrauliczne wydatku przelewów wykonuje się z wykorzystaniem wzorów, które są zbliżone do obliczeń wypływu cieczy z dużych otworów z częściowym wypełnieniem przepływającego strumienia.
Dla przelewów prostokątnych niezatopionych o ostrej krawędzi i kształtach praktycznych wydatek przepływu oblicza się ze wzorów:

•  przelew niezatopiony bez uwzględnienia prędkości dopływowej

•  dla przelewu zatopionego

gdzie :   α - wzniesienie zw. wody dolnej nad koroną przegrody,
              µ₁ i µ₂ -  współczynniki przepływu ustalone doświadczalnie.

Przy uwzględnieniu prędkości dopływającej (v_o) :

•  dla przelewu niezatopionego

•  dla przelewu zatopionego

Wstawiając   do   wzorów   współczynnik przelewu m=2/3μ  otrzymamy wzór zasadniczy na przelew zatopiony:

•  przy uwzględnieniu kontrakcji bocznej (n = 1 , n = 2) :

a) bez uwzględnienia prędkości dopływowej  k = v² / 2g

b) z uwzględnieniem prędkości dopływowej   k = v² / 2g  >1

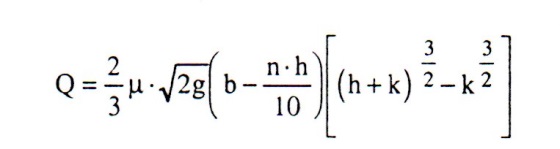
• przy braku kontrakcji bocznej (n=0) wzory przybierają postać:

a) bez uwzględnienia prędkości dopływowej  k = v² / 2g

            b) z uwzględnieniem prędkości dopływowej   k=v² / 2g  >1

Wartość współczynnika m można obliczyć ze wzorów doświad­czalnych Bazin-Hegly:

1.  dla przelewu z cienką ścianką, bez dławienia bocznego, tj. gdy b = B

2. dla przelewów z dławieniem bocznym tj. gdy b<B

3. dla przelewu zatopionego prostokątnego o ostrej krawędzi dla przypadku gdy h : p<0,7

Stąd wydajność przelewu w tych warunkach:

We wzorach tych oznaczono:   H - wzniesienie górnego zw. wody nad kra­wędzią przelewu,
                                                  α - wzniesienie dolnego zw. wody nad krawę­dzią przelewu,
                                                  p - wzniesienie krawędzi przelewu ponad dnem koryta,
                                                  h - różnica poziomów wody górnej i dolnej.

Z licznych wzorów empirycznych na określenie współczynnika wydatku przelewu prostokątnego na uwagę zasługuje kilka:

1.   Wzór Szwajcarskiego Stowarzyszenia Inżynierów i Architektów

2. wzór Rehbocka

3. wzór Fresego

Dla przelewu  trójkątnego  stosuje się wzór:

gdzie :  h — wzniesienie zw. wody ponad wierzchołkiem kąta, tj. najniższym punktem przelewu.

Przelewy o szerokiej koronie występują wtedy, gdy jej długość w kierunku przepływu wody jest równa:

L = (2 – 3) H

Rys. 7. Przelew o szerokiej koronie

Nad koroną takiego przelewu strugi cieczy układają się prawie równolegle, co sprawia, że warunki przepływu są bliskie ruchowi jednostajnemu i zmienia w ten sposób kryteria zatopienia przelewu o szerokiej koronie w stosunku do pozostałych przelewów.  Jeżeli przepływ nad koroną przelewu nie jest hamowany przez poziom wody dolnej, to nad koronąpowstaje ruch krytyczny, co z kolei powoduje, że zaburzenia strumienia nie mogą przenosić się w górę koryta. Wynika to z faktu, że obie prędkości krytyczna i posuwania się zaburzeń są równe. W tej sytuacji dolny poziom strugi ( w strefie poszuru) nie ma wpływu na wydatek przelewu. Przelew o szerokiej koronie jest zatopiony, gdy poziom dolny strugi przekroczy głębokość krytyczną h_p, odpowiadającą danemu przepływowi Q. Z rys. 7 wynikają dwa kryteria:

•   dla a  <  hp   przelew niezatopiony i
•   dla a  >  hp   przelew zatopiony.

Głębokość wody na przelewie h_p jest teoretycznie równa głębokości krytycznej, czyli 2/3 całkowitej energii płynącej cieczy E_c zgodnie ze wzorem :

gdzie :    h_kr  - głębokość krytyczna przelewu  m,
               H  -  wzniesienie poziomu cieczy nad krawędzią przelewu,
               E_c  -  wysokość energii jako suma :

              
               v_o² / 2g   - wysokość prędkości,
                v_o  - prędkość dopływającej cieczy m/s,
                α - współczynnik dławienia,
                g  - przyspieszenie ziemskie m/s².

W rzeczywistości głębokość h_p jest mniejsza od obliczonej  wzorem o ok. 5 – 15 % z uwagi na straty występujące przy przepływie nad przelewem.

Tab. 1. Współczynniki do obliczania przelewów o szerokiej koronie

Tab. 2.  Wartości współczynników dla przelewów o kształtach praktycznych

Należy pamiętać, że wzory dla przelewów o kształtach praktycznych i o ostrej krawędzi nie uwzględniają prędkości wody dopływającej w nurcie.
Chcąc uwzględnić ten wpływ na wynik obliczeń w podanych wzorach należy powiększyć wartość H o wysokość prędkości:

v_o² / 2g   - wysokość prędkości

Dla przelewów o kształtach praktycznych, gdy występuje kontrakcja boczna wydatek oblicza się ze wzorów:

•  przelew niezatopiony:

lub

gdzie:

             przy  h  =  H

•  przelew zatopiony :

lub 

gdzie

             przy  h  <  H

Symbole w tych wzorach oznaczają:
                    σ_zat   - współczynnik zatopienia w zależności od a/H ( tab. 3),
                    b’ = ε∙ b  - zdławiona szerokość strumienia między filarami,
                    ε  -  współczynnik dławienia bocznego,
                    b  -  światło przelewu

Wzór ten jest ważny, gdy H_o / b ⩽ 1. W przypadku gdy H_o / b > 1 należy zastosować uproszczony wzór wpisując jednocześnie wartość H_o / b = 1  :

gdzie:     n   -  ilość otworów przelewowych w jazie,
              ε_o , ε_k  -  współczynniki podane na rys. 8, dla różnych obrysów części wlotowej filarów

Rys. 8. Różne obrysy filarów wlotowych

Fot. Przelew o wielu filarach wlotowych

Tab. 3. Wartości współczynników zatopienia σ_zat dla przelewów o kształtach praktycznych

Współczynnik wydatku przelewu m = 2/3 μ w odróżnieniu od przelewów o ostrej krawędzi nie ma tutaj ustalonych ścisłych wartości. Przelewy o kształtach praktycznych mogą mieć różne kształty korony i tak przyjmuje się :

•  dla przelewów o kształtach prostokątnych i trapezowych  m = 0,40 – 043,
•  dla przelewów o kształtach krzywoliniowych m = 0,45 – 0,49,
•  dla obrysu wg współrzędnych Creagera  m = 0,49.

Wzór podany wcześniej:

należy stosować w przypadku, gdy w przelewie umieszczone są filary o jednakowym kształcie obrysów w częściach wlotowych jak również zbieżne są z kształtami filarów przyczółki. Wtedy ε_o i  ε_k  są jednakowe co do watości dla całego przelewu.

W przypadku gdy kształty filarów pośrednich w przelewie są różne od kształtów przyczółków (rys. 9), to wzór na ε przybiera postać :

gdzie :    ε_k1  ,  ε_k2  , ε_k3  - współczynniki dławienia bocznego wg rys. 9,
                 n₁  ,  n₂  ,  n₃  - liczba zdławionych stron strumienia.

Dla przypadku pokazanego na rys. 9 będzie to :

ε_k1 = 1 ,    n₁ = 2

ε_k2 = 0,4  ,   n₂  = 2

 ε_k3 = 0,7  ,   n₃ =  2

Rys. 9. Różne kształty filarów i przyczółków w przelewie

W przypadku gdy wartość A > 3 b H dla prostokątnych otworów przelewowych, to można nie uwzględniać prędkości dopływowej.
Wydatek dla przelewów o szerokiej koronie

•  przelew niezatopiony ( a < h_p):

•  przelew zatopiony ( a ≥ h_p):

gdzie :      m – współczynnik wydatku przelewu,
                 φ  - współczynnik prędkości,
                 k  -  współczynnik zgodnie z tab. 1

Wysokość warstwy na przelewie oblicza się ze wzoru :

h_p  =  k H_o

Przykład:      Obliczyć światło b przelewu. Poniżej przedstawiony zostanie najczęstszy tok obliczeń:

•  znany jest przepływ w rzece Q,
•  zakładamy projektowaną rzedną progu przelewu,
•  z krzywej konsumcyjnej przy znanym przepływie otrzymujemy poziom wody dolnej w korycie,

Rys. - Typowa krzywa przepływu (konsumcyjna)

•  stąd otrzymujemy wartość a jako różnicę pomiędzy rzędną wody dolnej i rzędną korony przelewu,
•  zakładamy wysokość piętrzenia H. Wynika ona z rzędnej obwałowania koryta lub też może być podyktowana innymi ograniczeniami natury fizycznej lub technicznej,
•  obliczamy v_o                                     v_o = Q / A
  gdzie:  A  =  f(H) jest to przekrój poprzeczny koryta przed przelewem przy napełnieniu H.
•  obliczamy                                         H_o= H + α v_o² / 2g    ,
•  korzystając z tab. 1 odczytujemy k dla danego przelewu, a następnie obliczamy          h_p = k ∙ H_o  .
•  w przypadku a <  h_p przelew jest niezatopiony i szerokość b  oblicza się ze wzoru :

• - w przypadku a >  h_p przelew jest zatopiony i szerokość b  oblicza się ze wzoru :

•  prędkości dopływowej można nie uwzględniać w przypadku :  A > 4 b H.

Przelewy boczne są to przelewy, których oś jest równoległa lub pod kątem nachylona do zasadniczego przepływu strug cieczy płynącej w korycie.

Rys. 10. Przykłady przelewów bocznych

Wydatek przelewu bocznego niezatopionego, gdy w korycie panuje ruch nadkrytyczny (rys. 10 b) oblicza się ze wzoru :

gdzie :    b  - szerokość przelewu,
              H = h₂ – a   - wysokość warstwy przelewającej się cieczy w końcu przelewu,
               a  - wzniesienie korony przelewu nad dnem koryta (Rys. 10a),
               m = 2/3 μ  -  współczynnik wydatku przelewu zależny od kształtu korony i jego średnia wartość może być przyjęta w granicach 0,4,
               σ_bocz  - współczynnik korygujący dla przelewu bocznego.

Współczynnik korygujący dla przelewu bocznego, wg Engelsa :

a dla przelewów zgodnie z rys. 10 c) i 10 d), gdy tg θ  =  1/40 – 1/3, to:

Literatura:

1. Bagiński R.: Budownictwo wodne. Cz. I – Hydrologia.PWN, Poznań 1954,
2. Buszma E., Domaradzki J., Rolla S.: Budowa dróg. Cz. I. PWSZ, Warszawa 1969,
3. Czyżewski K [i in.]: Zapory ziemne. Arkady, Warszawa 1973,
4. Fanti K. [ i in.]: Budowle piętrzące. Arkady, Warszawa 1972,
5. Kollis W. [i in.]: Przewodnik budownictwa wodno-melioracyjnego. PWRiL, Warszawa 1955,
6. Linder F.: Budowa mostów. Cz. I. PWSZ Warszawa 1970,
7. Lisowski K.: Hydraulika. PZWS, Poznań 1950,
8. Podniesiński A.: Zbiór zadań z hydrauliki. PWN, Warszawa 1958,
9. Szwed F.: Zarys budownictwa wodnego. PWN, Kraków 1952.