Przykład:


Przykład:
Wykop fundamentowy o wymiarach a = 20,0 m, b = 30,0 m sięga warstwy wodonośnej, w której znajduje się woda pod ciśnieniem. Statyczny poziom linii ciśnień H = 9,5 m. Miąższość warstwy wodonośnej a= 6,5 m. Dno wykopu wzniesione jest nad dolną warstwą nieprzepuszczalną na wysokość h = 5,0 m.
Współczynnik filtracji k = 0,001 m/s. Dookoła wykopu rozmieszczono 8 studni (patrz rysunek) obliczyć wydatek każdej studni, potrzebny dla osuszenia wykopu
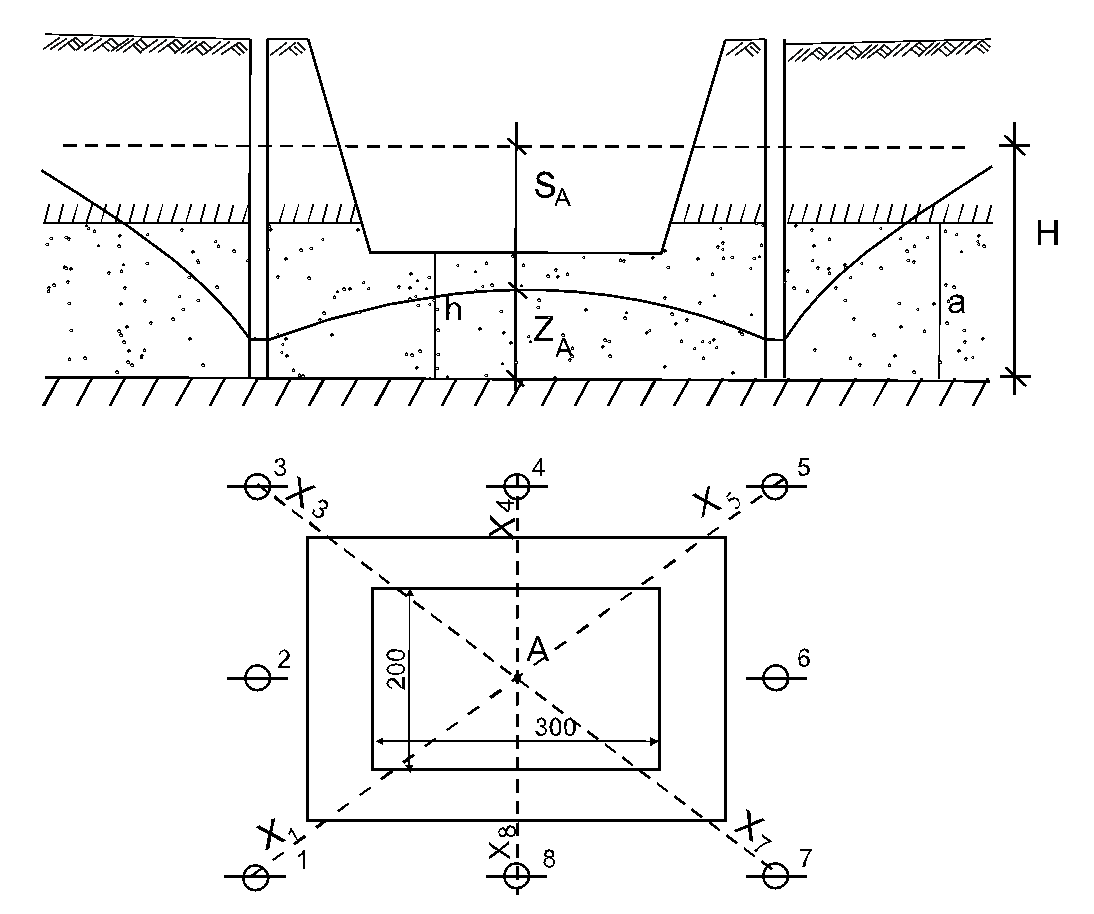
Łączny wydatek zespołu studni obliczamy ze wzoru:
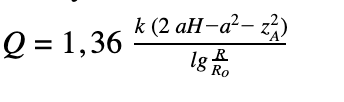
gdzie:

przy czym:
x - oznacza odległość od każdej studni do punktu A.

Przykład:
Obliczyć potrzebną liczbę studni depresyjnych dla odwodnienia wykopu o wymiarach w rzucie 22,0 x 37,0 m. Warunki gruntowo-wodne pokazano na rys. Wymagane obniżenie poziomu wody gruntowej poniżej dna wykopu 0,5 m.
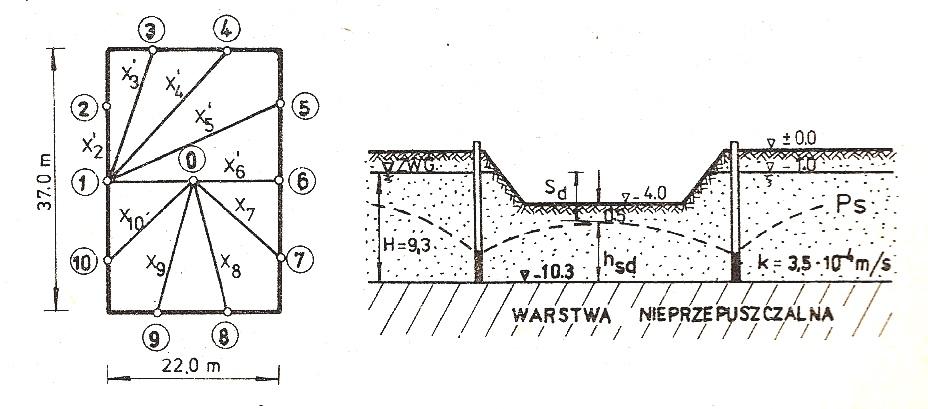
Rozwiązanie:
- Obliczanie liczby studni:
- promień okręgu równoważnego odwadnianej powierzchni (tzw. promień „dużej studni”)
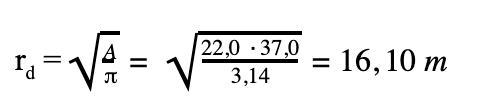
- wydatek „dużej studni”
H = -1,0 + 10,3 = 9,3 m, sd = -1,0 – (-4,0) + 0,5 = 3,5 m
hsd = 9,3 – 3,5 = 5,8 m
Ze wzoru Sichardta ( patrz strona 38):
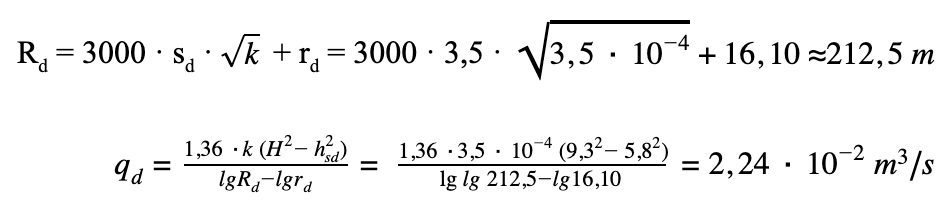
- wydatek pojedynczej studni depresyjnej, przyjmując promień filtra rf = 7,5 cm i jego długość hf = 4,0 m
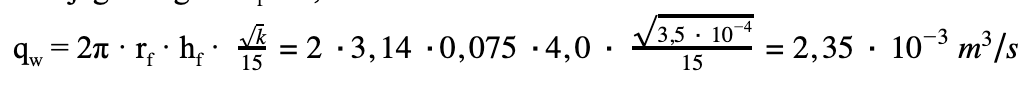
- liczba studni
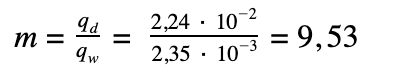
przyjęto m = 10 studni
- sprawdzenie minimalnej odległości między studniami
Lmin = 10 · π · rf = 10 · 3,14 · 0,075 = 2,36 m
rzeczywista odległość między studniami L = 10m > Lmin.
- Sprawdzenie poziomu zwierciadła wody w studniach depresyjnych (dla studni nr 1)
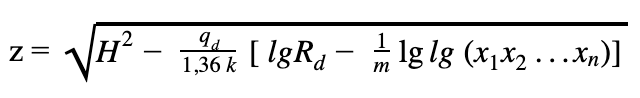
z – miąższość warstwy wody w rozpatrywanym punkcie po obniżeniu zwierciadła wody gruntowej,
qd – wydatek łączny grupy studni,
x1, x2, …xn – odległość rozpatrywanego punktu od studni.
Z rysunku : x1 = 0,075 x2,10 = 10,0 x3,9 = 19,4 x4,8 = 24,4 x5,7 = 24,2 x6 =22,0
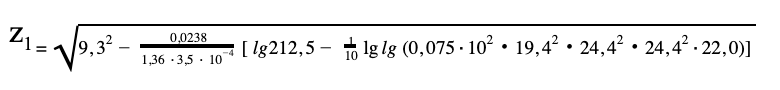
z1 = 4,67 m
hf = 4,0 m < z1 < hsd = 5,8 m.
- Sprawdzenie wymaganego obniżenia poziomu wody gruntowej w środku wykopu
Z rysunku : x1,6 = 11,0 x2,5,7,10 = 15,2 x3,4,8,9 = 19,2 m
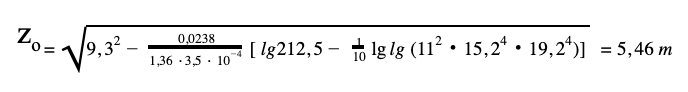
zo < hsd = 5,8 m
Można uznać przyjęty system odwodnienia za wystarczający.