Wypór jest to siła skierowana pionowo w górę, z jaką ciecz działa na zanurzone w niej ciało. Wielkość wyporu równa jest iloczynowi objętości ciała zanurzonego w cieczy i jej ciężaru objętościowego.
W = V ∙ g [kN]
Od dawna znany jest fakt, że jedne ciała pływają na wodzie, a inne toną. Prawa, jakim podlegają te zjawiska sformułował Archimedes. Na ciało zanurzone w cieczy działa siła zwana wyporem hydrostatycznym, skierowana pionowo do góry i równa jest ciężarowi cieczy wypartej przez to ciało. Aby zrozumieć prawo Archimedesa należy rozpatrzeć siły działające na ciało, zanurzone całkowicie w cieczy. Na powierzchnie boczne tego ciała o kształcie prostopadłościanu działają ciśnienia prostopadle do tych powierzchni, równe sobie co do wielkości, lecz przeciwnie skierowane. Ponieważ równoważą się one wzajemnie, ich wypadkowa jest równa zeru. Na górną powierzchnię ciała działają ciśnienia hydrostatyczne mniejsze niż na dolną (zagłębienie powierzchni górnej jest mniejsze niż dolnej). Parcie cieczy (tzn. suma ciśnień) na powierzchnię górną N1 jest więc mniejsze niż na powierzchnię dolną N2. Na ciało zanurzone działa więc różnica parć:
W = N2 – N1
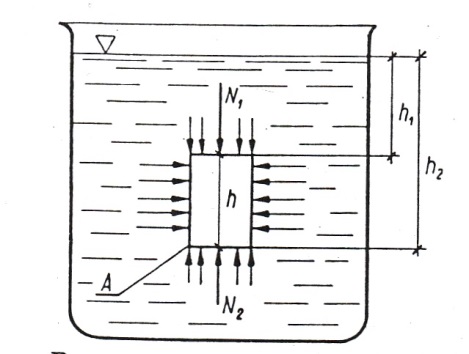
Rys. 1. Wykres ciśnień działających na ciało zanurzone w cieczy
Różnicę tę nazywamy wyporem hydrostatycznym. Wypór jest siłą skierowaną pionowo do góry. Definicja prawa Archimedesa brzmi następująco: Ciało zanurzone w cieczy traci - (pozornie) na swym ciężarze tyle, ile waży wyparta przez nie ciecz. Prawo Archimedesa znalazło praktyczne zastosowanie w rozwiązywaniu zagadnień związanych z pływaniem ciał, zwłaszcza z pływaniem statków. Z prawa Archimedesa wynika, że na ciało zanurzone w cieczy działają dwie siły: ciężar ciała G i wypór cieczy W (Rys. 1).
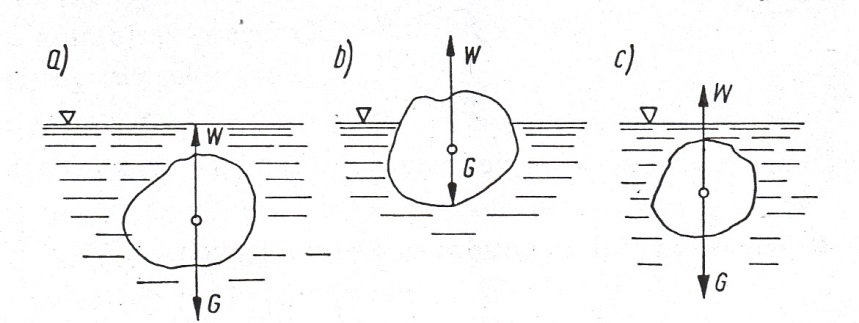
Rys. 2. Wykresy sił działających na ciało zanurzone: a) przy G=W, b) przy G<W, c) przy G>W
Zachodzą tu trzy przypadki zależności pomiędzy ciężarem ciała G a jego wyporem W.
1. Ciężar ciała G równa się wyporowi cieczy W (a).
G = W
Jeżeli ciężar ciała określimy jako G = V∙γ1 , a wypór cieczy W = V • γ2 , to po podstawieniu otrzymamy:
V∙γ1 = V∙γ2
czyli
γ1 = γ2
gdzie: V - objętość ciała równa objętości cieczy wypartej przez ciało,
γ1 - ciężar objętościowy ciała,
γ2 - ciężar objętościowy cieczy.
Ciało jest w stanie równowagi stałej, jeżeli jego ciężar objętościowy równa się ciężarowi objętościowemu cieczy. Ciało nie tonie i nie wypływa na powierzchnię.
2. Ciężar ciała jest mniejszy od wyporu cieczy (b), czyli G < W albo V∙γ1<V∙γ2, stąd wynika:
γ1 < γ2
to ciało pływa po powierzchni cieczy.
3. Ciężar ciała jest większy od siły wyporu (c)
G > W
lub γ1 > γ2
Ciało tonie w cieczy opadając na dno.
Warunek W = G jest konieczny, aby ciało nie tonęło w cieczy i nie wypływało. Aby jednak ciało znajdujące się w cieczy było w stanie równowagi, konieczne jest jeszcze spełnienie dodatkowych warunków. Stan równowagi ciała może być bowiem trwały, chwiejny lub obojętny i zależy od położenia tzw. metacentrum (mimośrodu), czyli punktu przecięcia się kierunku wyporu z osią pływania.
Oznaczając przez G środek ciężkości statku, a przez W środek jego wyporu, tj. środek ciężkości cieczy wypartej przez ciało (statek), otrzymujemy trzy stany równowagi. Odległość środka ciężkości ciała od metacentrum nazywa się wysokością metacentryczną.
Równowaga będzie tym trwalsza, im metacentrum będzie położone wyżej od środka ciężkości. Rysunek 3a) przedstawia stan równowagi trwałej ciała pływającego. Środek ciężkości ciała G znajduje się poniżej środka wyporu W. Linię przechodzącą przez środek ciężkości ciała G, skierowaną w stanie równowagi pionowo, nazywamy osią pływania, zaś punkt, w którym kierunek wyporu przecina oś pływania, metacentrum M. Okazuje się, że w razie wychylenia ciała z położenia równowagi oś pływania przyjmuje położenie pochyłe, a im odległość metacentrum od środka ciężkości ciała jest większa, tym trwalszy jest stan równowagi ciała. Jak widać z rysunku 3a) w stanie równowagi trwałej środek ciężkości G znajduje się poniżej środka wyporu W, odległość metacentrum M od środka G wzrasta z głębokością zanurzenia ciała (w tym przypadku - statku). Jest więc jasne, że przy prawidłowym załadunku statku należy przedmioty ciężkie umieszczać jak najbliżej dna statku oraz statek jak najbardziej obciążać, aby zwiększyć głębokość zanurzenia, a tym samym odległość metacentrum M od środka ciężkości G. Zapewnia to nie tylko trwałą równowagę, ale także zmniejsza przechylenie statku w razie burzy lub wysokiej fali. Jak widać z rysunku 3b), w przypadku równowagi chwiejnej środek wyporu W znajduje się poniżej środka ciężkości G, ciało wychylone z położenia takiej równowagi do niej już nie wróci. W stanie równowagi chwiejnej ciało (statek) ulegnie, pod wpływem momentu pary sił przeciwnie skierowanych, tj. ciężaru i wyporu, obrotowi wokół punktu M zgodnie z ruchem wskazówek zegara, aż do położenia, w którym środek ciężkości G znajdzie się pionowo pod środkiem wyporu W. Jak wskazuje rysunek 3b), tak niekorzystnie wysokie położenie środka ciężkości G byłoby możliwe tylko w razie niewłaściwego rozmieszczenia ładunku na pokładzie zamiast na dnie statku. W celu zapobieżenia temu umieszcza się we wnętrzu statku po wyładowaniu towarów tzw. balast, to jest jakiekolwiek obciążenie dla zapewnienia prawidłowej trwałej równowagi.
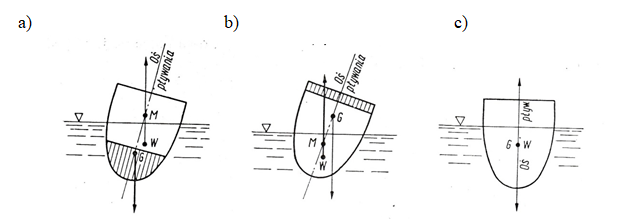
Rys. 3. Stany równowagi ciała pływającego: a) równowaga trwała, b) równowaga chwiejna, c) równowaga obojętna
Z kolei na rysunku 3c) zilustrowano warunki równowagi obojętnej, która zachodzi, kiedy środek ciężkości G i środek wyporu W pokrywają się. W takim przypadku występuje brak warunków ustalających pionowe położenie osi pływania, ciało jest w każdym położeniu w stanie równowagi, zarówno z pokładem na górze jak i pod wodą. Znajomość zjawisk związanych z wyporem dotyczy również wody gruntowej. W dużej ilości projektów znajdują się rozwiązania oparte na zbiornikach szczelnych bezodpływowych ze wskazaniem funkcji retencji, odparowania lub infiltracji. Przy tworzeniu szczelnej powierzchni zbiornika z geomembrany należy pamiętać również o zjawisku wyporu. Jeżeli poziom zwierciadła wody gruntowej znacznie przewyższa poziom dna zbiornika retencyjnego, to wystąpi wypór. Wyparcie gruntu jest to zjawisko polegające na przesunięciu wszystkich cząstek pewnej objętości gruntu podłoża w kierunku ruchu wody. Wskutek wyparcia grunt ulega rozluźnieniu, a jego właściwości - pogorszeniu. Wyparcie występuje na ogół w sposób nagły.
Przykład: Należy sprawdzić stateczność dna szczelnego zbiornika retencyjnego dla parametrów zgodnie z rysunkiem 4.
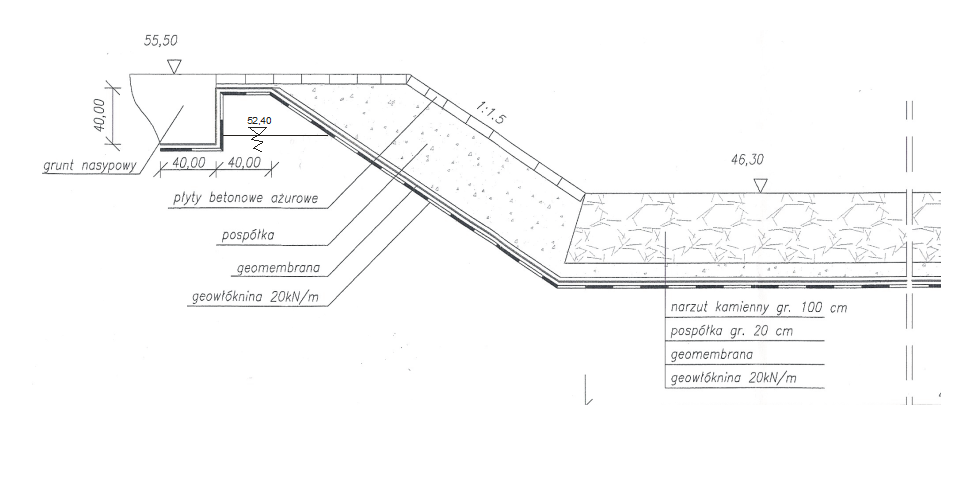
Rys. 4. Przekrój poprzeczny szczelnego zbiornika wodnego
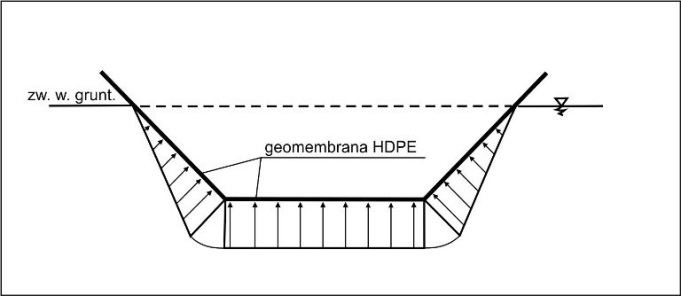
Rys.5. Wykresy sił parcia w dnie i na skarpach zbiornika szczelnego
Dane :
- rzędna dna wykopu zbiornika wynosi 45,10 m,
- poziom zw.w.g. układa się na rzędnej 52,40,
- grubość warstw przykrywających dno uszczelnionego zbiornika wynosi 1,20 m.
Ciężar warstw w dnie zbiornika wynosi łącznie : G = h1 ∙ g1 + h2 ∙ g2 = 1,0 ∙ 21,0 + 0,2 ∙ 19,0 = 24,8 kN
Wypór w dnie wynikający z różnicy poziomów zw.w.g. i dna zbiornika wynosi : W = (52,4 – 45,1) ∙ gw = 7,30 ∙ 10,0 = 73,0 kN
W >> G Warunek nie spełniony.
W niektórych znanych autorowi przypadkach, wykonawcy uszczelnień musieli ratować się przed niepożądanymi efektami wyporu, przedziurawieniem dna zbiorników wcześniej uszczelnionych geomembraną. Po ustaniu pracy igłofiltrów wokół takiego zbiornika zaczyna podnosić się poziom zdepresjonowanego zwierciadła wody gruntowej i geomembrana w dnie zaczyna „falować”. Bardzo często przedziurawienie dna ratuje sytuację i projektanta i wykonawcy robót uszczelnieniowych, gdyż wypór przy różnicy poziomów wody gruntowej i dna zbiornika wynoszącej ok. 5 m, to 50 kPa skierowane do góry. Praktycznie nie ma mowy o zrównoważeniu tej siły obsypką lub płytami drogowymi !
W takich przypadkach poziom wody w zbiornikach jest odzwierciedleniem poziomu wody gruntowej, a zbiorniki pełnią rolę trudną do ustalenia (Fot. 1).

Fot.1. Zbiornik z „rozszczelnieniem” powierzchni geomembrany w dnie